By Adian Samin
Edited By Pranomita Shom
Our universe is filled with tensors, from birds flying in the sky to the movement of celestial bodies in outer space; everything around us can be described using tensors.
Mathematicians often define a rank-𝑛 tensor in 𝑚 dimensions as a mathematical object that has 𝑛 indices and 𝑚^𝑛 components and obeys certain transformation rules. Although the definition is quite accurate and brief, it is a very abstract way to explain a tensor. Therefore, this article will explore what tensors truly are in depth.
Representation of tensors
The word tensor originates from the Latin word tendere, which means to stretch. If an object like a spring or a rubber band is stretched, it experiences tensile stress (𝜎) which results in extension. However, an object can undergo different kinds of stress. For example, a cube can be stretched in 3-dimensions and can also be sheared thus, there are 9 different stresses which can act on the cube.

The 9 different stresses acting on the cube is organized by a 3x3 matrix called a stress tensor:

The stress tensor above contains all the nine stresses that can act on the cube. To determine a component, we need only 2 elements: a row and a column. As the cube is in 3dimensions thus the tensor contains 3 rows and 3 columns.

Therefore, it is a rank-2(2 elements) dimension-3 tensor.
However, matrix and tensors are not the same. Here matrices are used to represent the 9 stresses in a convenient way.
Matrices are also used to represent other tensors such as the electromagnetic field tensor:

However, the matrix notation falls apart with higher rank tensor thus math operation becomes more complex, and the notation fails to represent the tensor in an effective way.


Thus, to overcome this problem mathematicians use index notation.

Tensor transformation
Let us think of a ball moving to the right. To use physics to quantify the movement of the ball a coordinate system must be assigned.
We can choose the coordinate system to be wherever we want to. Even rotation of the axes should not change physical reality.

The diagram below shows a vector which is a Rank-1 Dimension-2 Tensor. It has two components for each dimension, changing the coordinates will only change the value of the components but not the physical nature of the vector itself.
Since vectors are represented as an arrow it is plausible to think that the arrows (size of the vector) will not be affected by the change in a coordinate system. However, if we investigate the angular momentum of an object moving in a circular orbit this turns out to be false. Angular momentum is equal to the product of mass, radius, and velocity. 𝐿 = 𝑚𝑣𝑟.
If we place the coordinate system at the centre of the circular orbit the angular momentum always points upwards.
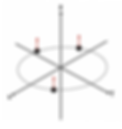
However, if we move the coordinate system to the edge of the circular orbit the angular momentum of the object changes with respect to time It even goes to 0 for a moment. This should not happen with a physical object therefore it is a false vector which is called a pseudovector. It has a direction thus it disguises itself as a vector. If a real vector is zero in one set of coordinates it must be zero in all of them.

It is also very reasonable to say that if we move the coordinate system along with the moving object the velocity becomes 0 and we can also say that velocity is a pseudovector. This is true in the case of a 3dimensional transformation however, to change it to a steadily moving coordinate system requires the use of an additional time axis as the object might move differently in relation to its surroundings and itself.
The ball is moving relative to the ground but not relative to itself. (space)

And thus, shifting to the moving coordinate system becomes a 4-dimensional coordinate rotation also known as a boost. Moreover, a rank-1 4-dimension tensor or 4-velocity vector is used to represent its motion as the object is now moving in 4-dimension and the 4-velocity is a real vector therefore unaffected by the rotation of axes.

Unfortunately, rank-2 tensors cannot be visualized as an arrow, but they can represent as a transformation between vectors as used in the Lorentz force law.

The tensor transforms the 4-velocity into a force. Therefore, a moving charge experiences a force in a magnetic field.

The stress tensor can also be used to find a force acting on the surface of an object such as a tetrahedron.

Here the area vector is transformed to a force vector by using a stress tensor.

From all the above examples shown tensors can now be described as a number or a collection of numbers that maintains their meaning under the transformation of coordinate systems just like the velocity vector or rank-1 tensor which describes the motion of an object and the stress tensor which describes how to get a force from an area regardless of the choice of coordinate system.
Note: if a number or collection of number does not retain its meaning under transformation it is a pseudotensor.
Usage of Tensor in bridging Geometry with Algebra
The mathematicians of ancient Greece used geometry in solving mathematical problems such as Heron’s problem and had a beautiful geometrical insight. However, after the discovery of calculus during the 1670s all geometrical problems were solved using calculus. Even though calculus was an immensely powerful tool used by great mathematicians and physicists like Euler and Lagrange, their solutions were deprived of the geometrical insight and lead to a lot of long and troublesome sets of equations unlike the mathematicians before the era of calculus had. As individually Geometry and Algebraic methods had their highs and lows, tensor analysis was the key to bridge the two ideas together. Tensor analysis also enabled us to ignore the choice of coordinate systems which had led to the unwelcomed artefact in the analytical solution and tensor analysis provides a framework for establishing equations valid in all coordinate systems. As we started our mathematical quests with the world of Geometry, which is beautiful but limited followed by the world of Analytical systems which is enormously powerful but lacks geometrical insight and generates unworkable expression. This is where tensor analysis comes in handy allowing us to do algebraic analysis with geometrical insight and brings a balance between Geometry and Algebra.